Data Science 2 (Regression)

Data Science 2 (Regression)#

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import cross_validate, train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

# Matplotlib parameters
plt.rcParams["figure.dpi"] = 150
plt.rcParams["figure.figsize"] = [4, 3]

Aufgabe 1: Einstieg#

Wir werden in diesem Aufgabenblatt im Kontext von Regressionsanalysen Overfitting und Underfitting untersuchen. Dafür arbeiten wir zunächst mit einem kleinen Beispiel-Datensatz, welcher zwei Attribute x und y beinhaltet:

# Datensatz einlesen
df = pd.read_csv("../resources/10_data_science/simple_regression.csv")

# Datensatz visualisieren
ax = df.plot(x="x", y="y", style="o")
ax.set_xlabel("x")
ax.set_ylabel("y")
plt.show()
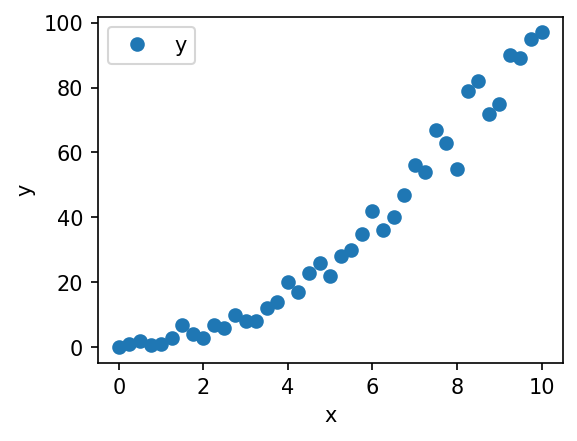
../_images/bd7e7cab60156a2524dee8ab5b8b64895660cae5b8b2986ac8ff27e5eecd1ed1.png

Fragen:#

  1. Wenn wir Attribut x verwenden wollen, um Vorhersagen zu Attribut y zu treffen, handelt es sich um Regression oder Klassifikation? Begründen Sie Ihre Antwort.

  2. Wie sähe Ihrer Meinung nach ein gutes Modell für diese Daten aus?

Aufgabe 2: Lineare Regression#

Wir bringen nun den Datensatz in eine Form, die von der scikit-learn Bibliothek verstanden wird. Dazu teilen wir die Attribute in zwei Numpy Arrays auf:

  1. Array X enhält alle unabhängigen Variablen (bei uns also nur x, sonst aber oft (deutlich) mehr als ein Attribut)

  2. Array y enhält die abhängige Variable (bei uns y)

Die Arrays haben die folgenden Dimensionen:

  • X hat Dimension Dimension \(N \times M\), wobei \(N\) die Zahl der Datenpunkte ist und \(M\) die Zahl der unabhängigen Attribute. Wir haben 41 Datenpunkte und nur ein unabhängiges Attribut, also \(N=41\) und \(M=1\).

  • y hat Dimension \(N \times 1\).

# Vorbereiten der Arrays
X = df[["x"]].values.reshape(-1, 1)
y = df[["y"]].values.reshape(-1, 1)

# Dimensionen des DataFrames und der Arrays anzeigen
df.shape, X.shape, y.shape

((41, 2), (41, 1), (41, 1))

Wir geben Ihnen nun eine Funktion vor, die für Sie im Folgenden hilfreich sein kann. Sie visualisiert die Vorhersagen eines Regressions-Modells:

def visualize_regression(model, X, y_true, figsize=(5, 4)):
    """Visualisiert die Vorhersagen eines gegebenen Regressions-Modells auf einem gegebenen Datensatz."""
    # Fortlaufende x-Werte generieren (um eine Linie zu zeichnen)
    fit_X = np.reshape(np.arange(np.min(X), np.max(X), 0.1), (-1, 1))
    # Modell-Vorhersagen für diese x-Werte generieren
    fit_y = model.predict(fit_X)

    # Datensatz plotten (als Punkte)
    plt.figure(figsize=figsize)
    plt.scatter(X, y_true)

    # Modell-Vorhersagen plotten (als rote Linie)
    plt.plot(fit_X, fit_y, color="red")
    plt.show()

Wir erstellen nun mit linearer Regression ein Modell für unseren Datensatz. Dazu verwenden wir die Implementierung von Linearer Regression, die scikit-learn bereitstellt:
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html

lr = LinearRegression()
model_1 = lr.fit(X, y)

Aufgabe 2.1 Visualisierung des Modells#

Visualisieren Sie das Modell. Nutzen Sie dazu die visualize_regression Funktion.

  • Beschreiben Sie, was Ihnen auffällt.

  • Halten Sie das Modell für geeignet, um über y Vorhersagen zu treffen? Warum bzw. warum nicht?

  • Haben Sie Ideen, wie man das Modell verbessern könnte?

Notiz: Im Code von visualize_regression können Sie sehen, wie model.predict() genutzt wird, um Modell-Vorhersagen für Daten zu treffen. Dies können Sie auch mit eigenen Daten ausprobieren. Es ist am Anfang nur etwas irritierend, die Daten in das richtige Array-Format zu bringen.

Hier ein Beispiel: wenn Sie eine Vorhersage für \(x=100\) machen wollen, geht das z.B. so: model_1.predict(np.array([[100]])).

# your code goes here

Fragen#

  1. Was fällt Ihnen auf? Halten Sie das Modell für geeignet, um Vorhersagen für y zu treffen?

  2. Haben Sie Ideen, wie man das Modell verbessern könnte?

Aufgabe 3: polynomielle (lineare) Regression#

Wir werden das Modell nun verbessern, indem wir polynomielle Regression verwenden. Dazu ist es üblich, das Datenset mit polynomiellen Attributen zu erweitern und dann lineare Regression auf dem erweiterten Datenset durchzuführen.

Scikit-learn stellt diese Funktion über PolynomialFeatures bereit.

Zum Verständnis untersuchen wir uns zunächst, wie diese polynomiellen Attribute aussehen. Dazu betrachen wir, wie PolynomialFeatures mit dem Parameter degree=2 die ersten 3 Datenpunkte in X verändert. Der Parameter 2 bestimmt, dass alle Polynome bis Grad 2 hinzugefügt werden, also \(x^0\), \(x^1\) (was schon existiert), und \(x^2\). Laut Dokumentation erstellt PolynomialFeatures(degree=2) aus einem Datenset mit einem Attribut \(x\) die Attribute \(1\), \(x\), \(x^2\) (\(1\) ist ein konstanter “Intercept”):

# Die ersten drei Datenpunkte in X
X[:3]

array([[0.  ],
       [0.25],
       [0.5 ]])

# Die ersten drei Datenpunkte in X mit polynomiellen Attributen
# Die Spalten sind: x^0, x^1, x^2
PolynomialFeatures(degree=2).fit_transform(X)[:3]

array([[1.    , 0.    , 0.    ],
       [1.    , 0.25  , 0.0625],
       [1.    , 0.5   , 0.25  ]])

Aufgabe 3.1 Good Fit#

Finden Sie ein gutes Modell, probieren Sie dazu verschiedene Werte für degree und visualisieren Sie die entstehenden Modelle.

  • Welchen Degree halten Sie am besten für diesen Datensatz geeignet?

Wir verwenden im Folgenden eine Pipeline, um das Hinzufügen von Attributen und die Lineare Regression zu kombinieren. Den Code dazu haben wir Ihnen vorgegeben.
Sorgen Sie dafür, dass in pipeline_good_fit eine Pipeline mit einem guten Wert für degree gespeichert ist. Die Pipeline werden wir später weiter verwenden.

# Pipeline vorbereiten
pipeline_good_fit = Pipeline(
    [
        ("poly", PolynomialFeatures(degree=1)),  # TODO: Degree verändern
        ("linear", LinearRegression()),
    ]
)

# Ein Modell für unser Datenset lernen
model_good_fit = pipeline_good_fit.fit(X, y)

# TODO: visualisieren

Aufgabe 3.2 Overfitting#

Overfitten Sie das Modell. Probieren Sie auch hierzu verschiedene Werte für degree aus.

Sorgen Sie dafür, dass die Pipeline in pipeline_overfit overfitted. Auch diese Werden wir später noch verwenden.

# Pipeline vorbereiten
pipeline_overfit = Pipeline(
    [
        ("poly", PolynomialFeatures(degree=1)),  # TODO: Degree verändern
        ("linear", LinearRegression()),
    ]
)

# Ein Modell für unser Datenset lernen
model_overfit = pipeline_overfit.fit(X, y)

# TODO: visualisieren

Aufgabe 4: Modell-Evaluierung#

Subjektive, visuelle Evaluierungen sind eine Möglichkeit, Modelle zu evaluieren. Objektive Metriken geben aber oft eine besseres Bild. Im Folgenden werden wir dafür die Metrik mean squared error (MSE, deutsch: mittlere quadratische Abweichung) verwenden. Diese wird sehr häufig für Regressionsanalysen verwendet. Die Formel für den MSE ist:

\[MSE(\mathbf{y}, \mathbf{\hat y}) = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat y_i)^2\]

Zur Notation:

  • \(\mathbf{y}\) steht für den Vektor der korrekten Zielwerte.

  • \(\mathbf{\hat y}\) steht für den Vektor der von einem Modell vorhergesagten Werte.

  • In unserem Code haben wir für \(\mathbf{y}\) bisher y geschrieben und y_pred für \(\mathbf{\hat y}\) (sonst ist oft auch y_hat üblich).

  • \(y_i\) steht für den “i-ten” Eintrag in Vektor \(\mathbf{y}\).

  • \(N\) ist die Zahl der Datenpunkte (also die Länge der Vektoren \(\mathbf{y}\) und \(\mathbf{\hat y}\)).

Aufgabe 4.1 MSE#

Berechnen Sie zunächst von Hand den MSE für ein einfaches Beispiel:

\[\mathbf{y} = (2, 1, -3)\]
\[\mathbf{\hat y} = (1, 1, 2)\]

Aufgabe 4.2 Evaluation#

Evaluieren Sie die Modelle, die Sie oben erstellt haben. Berechnen Sie hierzu den MSE für die Modelle auf unserem Datensatz und vergleichen Sie die Werte.

  • Welches Modell funktioniert laut dieser Metrik am besten?

  • Sehen Sie Probleme mit dieser Evaluierungsstrategie? Wenn ja, welche?

Nutzen Sie für die Berechnung des MSE die scikit-learn Funktion mean_squared_error.

Erinnerung: Sie können Modell-Vorhersagen mit model.predict(X) erzeugen.

# your code goes here

Aufgabe 5: Test/Train-Split#

Wir werden nun den Datensatz in zwei Teile, “train” und “test”, aufteilen, um zu vermeiden, dass auf demselben Datensatz trainiert und evaluiert wird. Wir erhalten zwei Datensätze:

  • Für Modell-Training: X_train + y_train

  • Für die Evaluation: X_test + y_test

Mehr Informationen zu Training/Validation/Test split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=25)

Aufgabe 5.1#

Trainieren Sie die verschiedenen Modelle auf dem Train-Split und evaluieren Sie die trainierten Modelle anschließend auf dem Test-Split.

  • Welches Modell ist mit dieser Methodik das “beste”?

Hinweis: Sie können mit some_pipeline.fit(X_todo, y_todo) neue Modelle trainieren und nach wie vor über model.predict(X_todo) Vorhersagen machen.

# your code goes here

Exkurs: Kreuzvalidierung*#

Zur Evaluierung wird oft Kreuzvalidierung verwendet. In scikit-learn geht dies einfach über model_selection.cross_validate.

Aufgabe: Evaluieren Sie die obigen Modell mit Kreuzvalidierung. Wählen Sie hierzu frei die Zahl der Folds.

  • Welches Modell ist mit Kreuzvalidierung das “beste”?

# your code goes here
Contents