Data Science 1 (k-Means Clustering)#
In den letzten beiden Vorlesungsthemen setzen wir uns mit Data Science auseinander. Data Science beruht auf Maschinellem Lernen, welches sich grob in drei Klassen unterteilen lässt: Unsupervised Learning, Supervised Learning und Reinforcement Learning. Wir beschäftigen uns in diesem Tutorium spezifisch mit Unsupervised Learning, ehe wir uns in der kommenden Woche mit Supervised Learning auseinandersetzen.
Das Tutorium in dieser Woche besteht aus zwei Jupyter Notebooks. In diesem Notebook behandeln wir zuerst k-Means Clustering, ehe wir uns im zweiten Notebook mit Hierarchischen Clustering beschäftigen. Wir empfehlen Ihnen, die Notebooks Aufgabe für Aufgabe durchzuarbeiten, da viele Aufgaben auf vorherigen Aufgaben aufbauen.
In den Data Science Tutorien benutzen wir verstärkt externe Bibliotheken für die Implementierung der Inhalte. Wir empfehlen Ihnen, sich mit diesen Bibliotheken (insbeonsdere Numpy, Pandas, scikit-learn und matplotlib) auseinanderzusetzen. Das ist allerdings keine Voraussetzung für die Prüfungsleistungen in ISDA.
Hinweis: Aufgaben, die durch einen Asterisk (*) markiert sind, sind Bonusaufgaben. Diese Aufgaben können im Tutorium behandelt werden, dies ist jedoch von den Übungsleitern nicht geplant.
import copy
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
# Matplotlib parameters
plt.rcParams["figure.dpi"] = 150
plt.rcParams["figure.figsize"] = [4, 3]
plt.rcParams["font.size"] = 8
Aufgabe 1: k-Means von Hand#
Datenpunkte#
Zuerst generieren wir 8 Datenpunkte, welche wir als toy_data abspeichern.
toy_data = pd.DataFrame({"x": [2, 2, 4, 4, 6, 6, 8, 8], "y": [2, 4, 2, 4, 6, 8, 6, 8]})
toy_data.style.hide(axis="index")
| x | y |
|---|---|
| 2 | 2 |
| 2 | 4 |
| 4 | 2 |
| 4 | 4 |
| 6 | 6 |
| 6 | 8 |
| 8 | 6 |
| 8 | 8 |
Start-Centroids#
Zusätzlich generieren wir 2 Start-Centroids.
centroids = pd.DataFrame({"x": [2, 4], "y": [1, 1]})
centroids.style.hide(axis="index")
| x | y |
|---|---|
| 2 | 1 |
| 4 | 1 |
Startzustand visualisiert#
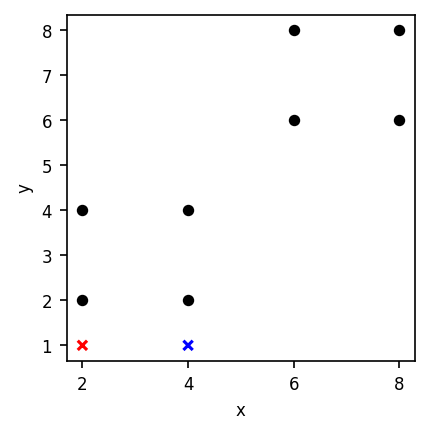
Aufgabe: Führen Sie auf dem Datensatz toy_data k-Means aus, bis die Centroids konvergiert sind.
ax = toy_data.plot.scatter(x="x", y="y", c="black", figsize=(3, 3))
centroids.plot.scatter(x="x", y="y", c=["red", "blue"], ax=ax, marker="x")
plt.show()
Aufgabe 2: k-Means implementieren#
Ihre Aufgabe ist nun, k-Means selbst zu implementieren. Hierzu werden Sie Code-Gerüste (siehe unten) ergänzen.
Gegeben ist eine Funktion, die ein Clustering visualisiert (siehe unten), und eine Funktion, die zufällige initiale Centroids generiert. Weitere Informationen sind im Code als Kommentare enthalten.
Sie können Ihren Code zunächst mit dem Beispiel aus der Handsimulation testen (toy_data). Weiter unten führen wir einen größeren Datensatz mit 500 Datenpunkten ein.
def visualize_kmeans(data, centroids, assignments, figsize=(2.5, 2.5)):
"""
Visualisiert ein 2-dimensionales k-Means Clustering (Spaltennamen "x" und "y"). Die Funktion zeichnet einen Plot,
der die Datenpunkte und die Centroids enthält. Datenpunkte sind nach Centroid-Zuordnung gefärbt.
Argumente:
data: eine Matrix mit Dimension N x 2. Jede Zeile enthält einen von N Datenpunkten.
centroids: eine Matrix mit Dimension K x 2. Jede Zeile enthält einen von K Centroids.
assignments: Ein Vektor mit N Zeilen. Jede Zeile enhält die Cluster-Zuordnung für den jeweiligen Datenpunkt (0 bis M-1).
figsize: Ein Tupel mit der Größe des Plots (default: (3, 3)).
"""
plt.figure(figsize=figsize)
all_data = data.copy()
all_data["assignments"] = assignments.astype("int")
all_data["assignments"] = all_data["assignments"].astype("category")
groups = all_data.groupby("assignments", observed=False)
for centroid, group in groups:
plt.plot(
group["x"],
group["y"],
marker="o",
linestyle="",
label=centroid,
zorder=1,
markersize=5,
)
plt.scatter(
centroids[centroid, 0],
centroids[centroid, 1],
marker="s",
edgecolors="black",
s=40,
zorder=2,
)
plt.legend()
plt.grid(visible=True, which="both", axis="both")
plt.xlabel("x")
plt.ylabel("y")
plt.title(str(centroids.shape[0]) + " clusters")
plt.tight_layout()
plt.show()
def random_centroids(data, count):
"""Generiert zufällige Centroids für k-Means aus den Datenpunkten."""
mean = np.mean(data, axis=0)
var = np.var(data, axis=0)
centroids = np.zeros((count, 2))
for i in range(count):
centroids[i][0] = mean.iloc[0] + np.random.uniform(-1, 1) * var.iloc[0]
centroids[i][1] = mean.iloc[1] + np.random.uniform(-1, 1) * var.iloc[1]
return centroids
Aufgabe 2.1: Ihre Implementierung#
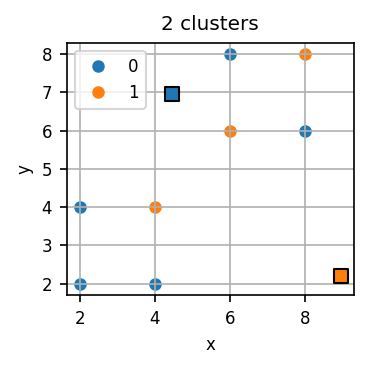
Gegeben sei der vorherige Datensatz und ein zufälliger Startzustand zweier Centroids. Den Startzustand lassen wir im unten stehenden Codeblock generieren und lassen dann erneut den Datensatz als auch die Centroids visualisieren.
Die k-Means-Implementierung basiert auf zwei zentralen Funktionen: assign_to_centroids() und new_centroids(). Unten finden Sie Beschreibungen und Gerüste für beide Funktionen. Ihre Aufgabe ist es, diese zu vervollständigen.
# Generierung zufälliger Centroids
num_centroids = 2
initial_centroids = random_centroids(toy_data, num_centroids)
# Zufällige initiale Zuordnungen
initial_assignments = np.random.randint(num_centroids, size=toy_data.shape[0])
visualize_kmeans(toy_data, initial_centroids, initial_assignments)
Nun müssen Sie noch die beiden Funktionen assign_to_centroids() und new_centroids() implementieren, um eine Iteration von k-Means durchführen zu können.
def assign_to_centroids(data, centroids):
"""
Berechnet für gegebene Datenpunkte und Centroids neue Centroid-Zuordnungen.
Argumente:
data: eine Matrix mit Dimension N x 2. Jede Zeile enthält einen von N Datenpunkten.
centroids: eine Matrix mit Dimension M x 2. Jede Zeile enthält einen von M Centroids.
Rückgabe:
Ein Vektor mit N Zeilen. Jede Zeile enhält die Cluster-Zuordnung für den jeweiligen Datenpunkt (0 bis M-1).
"""
assignments = np.zeros((data.shape[0],))
# Hilfestellung (muss nicht verwendet werden):
for i in range(data.shape[0]):
distance = np.zeros((centroids.shape[0], 1))
for j in range(centroids.shape[0]):
# your code here
print("Noch nicht implementiert")
return assignments
# Potentiell hilfreiche Funktionen:
# np.linalg.norm(point1 - point2) -- berechnet die Distanz zwischen zwei Punkten
# np.argmin() -- bestimmt den Index, dessen Wert minimal ist entlang einer Dimension (0 or 1 in unserem Fall)
def new_centroids(data, old_centroids, assignments):
"""
Berechnet für gegebene Datenpunkte und Centroid-Zuordnungen neue Centroids.
Argumente:
data: eine Matrix mit Dimension N x 2. Jede Zeile enthält einen von N Datenpunkten.
old_centroids: eine Matrix mit Dimension M x 2. Jede Zeile enthält einen M Centroids.
assignments: ein Vektor mit N Zeilen. Jede Zeile enthält die Zuordnung für einen Datenpunkt (0 bis M-1).
Rückgabe:
eine Mx2 Matrix. Jede Zeile enthält die (neuen) Koordinaten eines Centroids.
"""
centroids = old_centroids
for i in range(old_centroids.shape[0]):
# your code here
print("Noch nicht implementiert")
return centroids
# Potentiell hilfreiche Funktionen:
# np.mean() -- berechnet den Mittelwert entlang der angegebenen Dimension (0 oder 1 in unserem Fall)
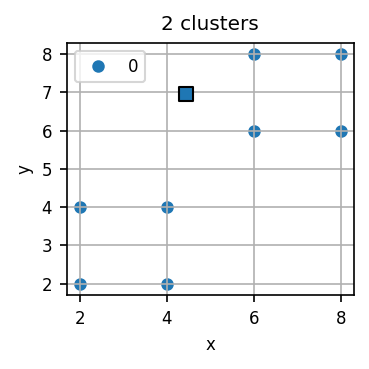
Mit diesem Startzustand können Sie nun eine Iteration von k-Means durchführen.
# Eine k-Means-Iteration
assignments = assign_to_centroids(toy_data, initial_centroids)
centroids = new_centroids(toy_data, initial_centroids, assignments)
visualize_kmeans(toy_data, centroids, assignments)
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Aufgabe 2.2: k-Means auf größerem Datensatz ausführen#
Wir laden nun einen größeren Datensatz. Ihre Aufgabe ist es, mit Ihrer k-Means Implementierung einige k-Means-Iterationen auf diesem Datensatz laufen zu lassen. Visualisieren Sie das Clustering zu Beginn und nach jeder Iteration. Wie viele Cluster halten Sie für sinnvoll?
# Datensatz laden
data = pd.DataFrame(
np.loadtxt("../resources/10_data_science/cluster.dat", dtype="float64").T,
columns=["x", "y"],
)
print(
f"Dimension des Datensets: {data.shape[0]} Zeilen, {data.shape[1]} Spalten mit Shape {data.shape}"
)
data.head()
Dimension des Datensets: 500 Zeilen, 2 Spalten mit Shape (500, 2)
| x | y | |
|---|---|---|
| 0 | 2.195194 | 0.119758 |
| 1 | 0.652289 | -0.565997 |
| 2 | 1.029164 | -0.078276 |
| 3 | -1.095304 | -0.777123 |
| 4 | 1.972860 | 0.830741 |
# your code here
Aufgabe 2.3: Mehrere Iterationen von k-Means*#
Ergänzen Sie unten die Funktion run_kmeans(), um das Ausführen mehrerer k-Means-Iterationen zu automatisieren. Die Funktion soll eine gegebene Zahl von k-Means-Iterationen durchführen.
def run_kmeans(data, centroids, iterations):
"""
Führt eine gegebene Zahl von k-Means-Iterationen durch.
Argumente:
data: Datenset (Nx2)
centroids: Initiale Centroids (Kx2)
iterations: Zahl der durchzuführenden Iterationen
Rückgabe:
Eine Liste von neuen Centroids
"""
# your code here
print("Noch nicht implementiert")
return centroids
Aufgabe 2.4*: k-Means mit Stop-Kriterium#
Da die Zahl der benötigten Iterationen in der Regel vor dem Clustering nicht bekannt ist, wird für k-Means oft mit einem Stop-Kriterium gearbeitet. Ihre Aufgabe ist nun, eine Variante der Funktion run_kmeans() zu implementieren, die mit solch einem Kriterium selbst entscheidet, wie viele Iterationen sie ausführen will.
Hinweis: Ein mögliches Stop-Kriterium sind die Veränderungen der Centroids von einer Iteration zur nächsten. Es sind aber auch andere Varianten denkbar.
def kmeans_stop(data, centroids):
"""
Führt k-Means aus und terminiert selbstständig, wenn ein Stop-Kriterium erfüllt ist.
Argumente:
data: Datenset (Nx2)
centroids: Initiale Centroids (Kx2)
Rückgabe:
Eine Liste von neuen Centroids
"""
# your code here
print("Noch nicht implementiert")
num_iterations = -1
assignments = -1
return (centroids, num_iterations, assignments)
Aufgabe 2.5: Die Grenzen von k-Means#
Setzen Sie die initialen Centroids manuell. Ist es möglich, Startpunkte so zu wählen, dass k-Means kein sinnvolles Clustering findet?
# Centroids manuell setzen
x1 = 0
y1 = 0
x2 = 0
y2 = 0
centroids = np.array([[x1, y1], [x2, y2]], dtype="float64").T
# k-Means implementierung aus Aufgabe 2.1 zum Visualisieren
num_centroids = 2
initial_centroids = centroids
initial_assignments = np.random.randint(num_centroids, size=toy_data.shape[0])
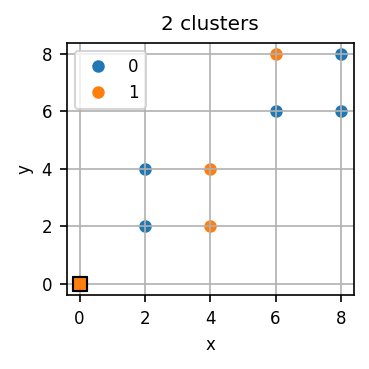
visualize_kmeans(toy_data, initial_centroids, initial_assignments)
# Eine k-Means-Iteration durchführen
assignments = assign_to_centroids(toy_data, initial_centroids)
centroids = new_centroids(toy_data, initial_centroids, assignments)
visualize_kmeans(toy_data, centroids, assignments)
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
Noch nicht implementiert
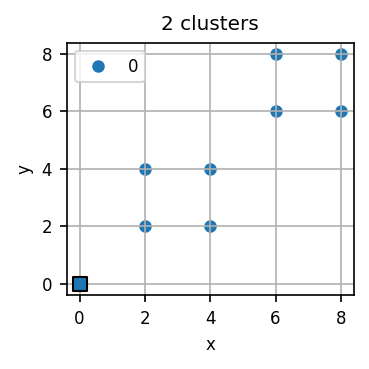
Ein sinnvolles Clustering ist bei einem k-Means-Algorithmus in der Praxis nicht immer direkt erkennbar. Mit zunehmender Dimensionalität wird unser intuitives Verständnis von “Nähe” und “Distanz” ungenau. Datenpunkte, die in einer Dimension weit voneinander entfernt scheinen, können in anderen Dimensionen sehr nah beieinander liegen.
Hinzu kommt, dass der k-Means-Algorithmus bestimmte Annahmen über die Form der Cluster macht: Er bevorzugt kugelförmige, in etwa gleich große und gleich dichte Cluster. In realen Datensätzen sind die Cluster jedoch häufig unregelmäßig geformt, unterschiedlich groß oder überlappend, was dazu führen kann, dass k-Means trotz korrekter Berechnung keine inhaltlich überzeugenden Gruppen bildet. Die Interpretation erfordert oft Domänenwissen.
Aufgabe 2.6: Ellenbogen-Methode#
Die Ellenbogen-Methode ist eine weit verbreitete Heuristik, um die Zahl der Cluster (k) zu bestimmen.
Der untenstehende Code führt zunächst für verschiedene k jeweils mehrere k-Means-Durchläufe durch und visualisiert für jedes k das errechnete Clustering für einen dieser Durchläufe.
Lassen Sie den Code laufen und untersuchen Sie die Visualisierungen. Wie viele Cluster halten Sie für dieses Datensatz für sinnvoll?
Wir verwenden hierzu die k-Means-Implementierung von scikit-learn. Sie können natürlich auch Ihre Implementierung nutzen. Diese läuft eventuell etwas langsamer.
max_k = 10 # maximale zu testendes k
n = 5 # Zahl der durchgeführten Clusterings pro k
score = np.zeros((max_k, n))
iterations = np.zeros((max_k, n))
threshold = 1e-4
# Wir probieren k=1..max_k
for i in range(0, max_k):
k = i + 1
# n Durchläufe für jedes k
for j in range(n):
# k-Means laufen lassen für dieses k, startet mit zufälligen Centroids
kmeans_model = KMeans(n_clusters=k, tol=threshold, init="random", n_init="auto").fit(data)
assignments = kmeans_model.labels_
centroids = kmeans_model.cluster_centers_
# (für später) Wir notieren für diesen Durchlauf (1) den Abstand der Punkte zu ihren Centroids
score[i][j] = kmeans_model.inertia_
# und (2) die Zahl der Iterationen, die k-Means durchgeführt hat
iterations[i][j] = kmeans_model.n_iter_
# Wir visualisieren den letzten der Durchläufe für dieses k
visualize_kmeans(data, centroids, assignments)
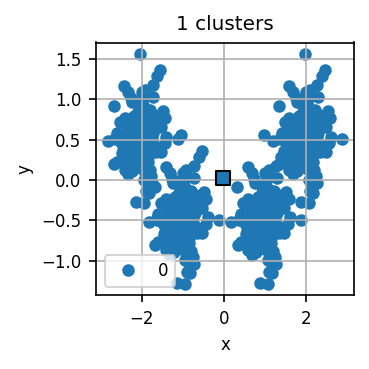
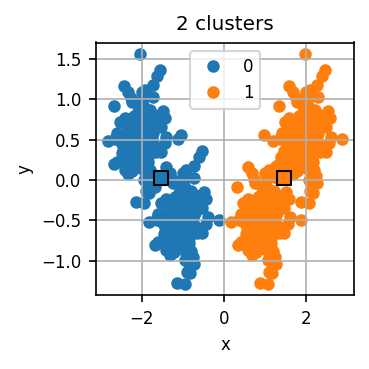
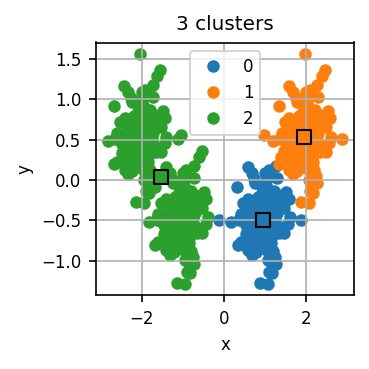
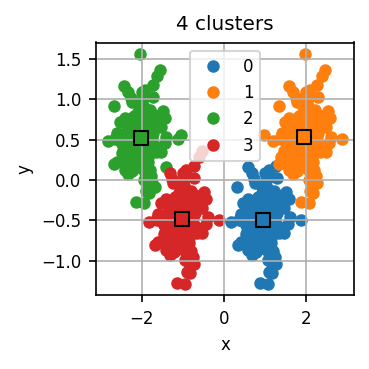
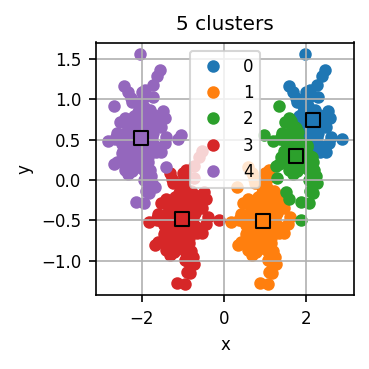
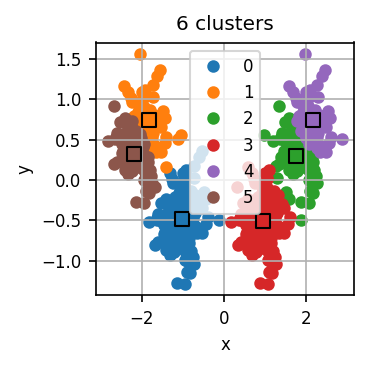
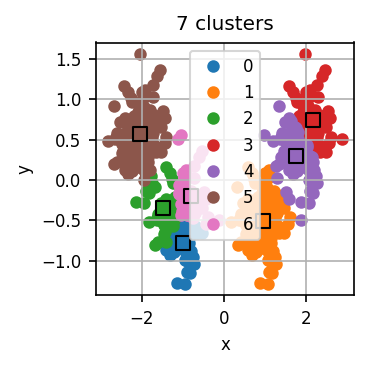
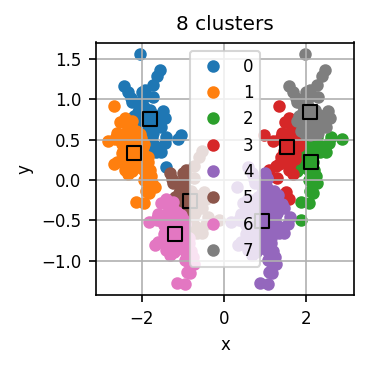
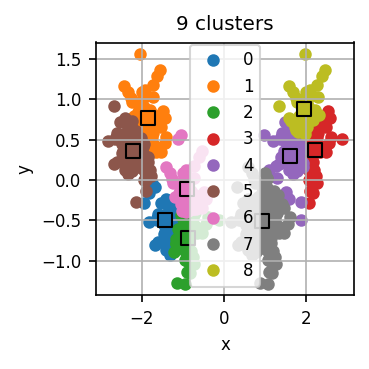
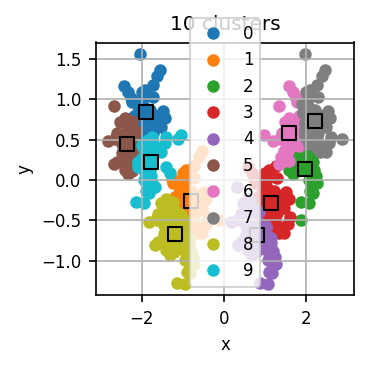
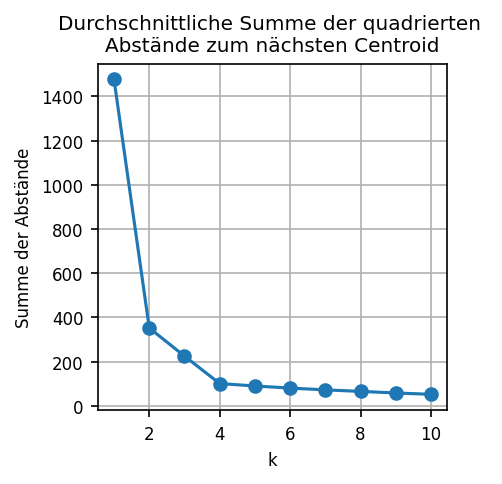
Nun wenden wir die Ellenbogen-Methode an. Für jeden Durchlauf hat der Code eine Art “Qualität” des entstandenen Clusterings errechnet. Dazu misst er die Distanz jedes Datenpunkts zum nächsten Centroid. Diese Distanzen quadrieren wir und summieren dann die quadrierten Distanzen aller Datenpunkte. Je kleiner diese Summe, desto “genauer” fassen die Centroids den Datensatz zusammen. scikit-learn erledigt dies automatisch und stellt uns diese Summe im Attribut inertia_ des Modell-Objekts bereit.
Wie viele Cluster halten Sie jetzt für sinnvoll?
Warum führen wir mehrere Durchläufe für jedes k durch? Was passiert, wenn wir dies nicht tun?
plt.figure(figsize=(3, 3))
plt.plot(
np.arange(1, max_k + 1),
np.mean(score, axis=1)[:,],
"o-",
)
plt.grid(visible=True, which="both", axis="both")
plt.xlabel("k")
plt.ylabel("Summe der Abstände")
plt.title("Durchschnittliche Summe der quadrierten \nAbstände zum nächsten Centroid")
plt.show()
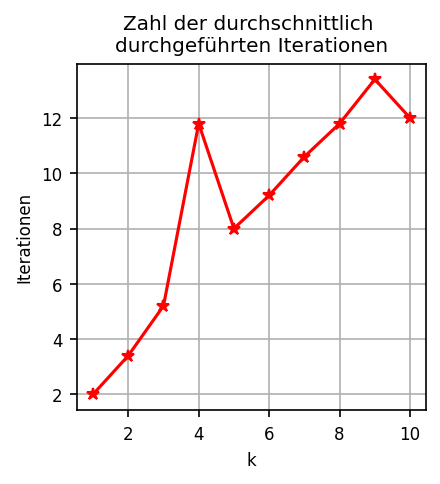
Wie ändert sich die Zahl der ausgeführten Iterationen, wenn wir k erhöhen? Warum?
plt.figure(figsize=(3, 3))
plt.plot(
np.arange(1, max_k + 1),
np.mean(iterations, axis=1)[:,],
"*-",
color="red",
)
plt.grid(visible=True, which="both", axis="both")
plt.xlabel("k")
plt.ylabel("Iterationen")
plt.title("Zahl der durchschnittlich \ndurchgeführten Iterationen")
plt.show()
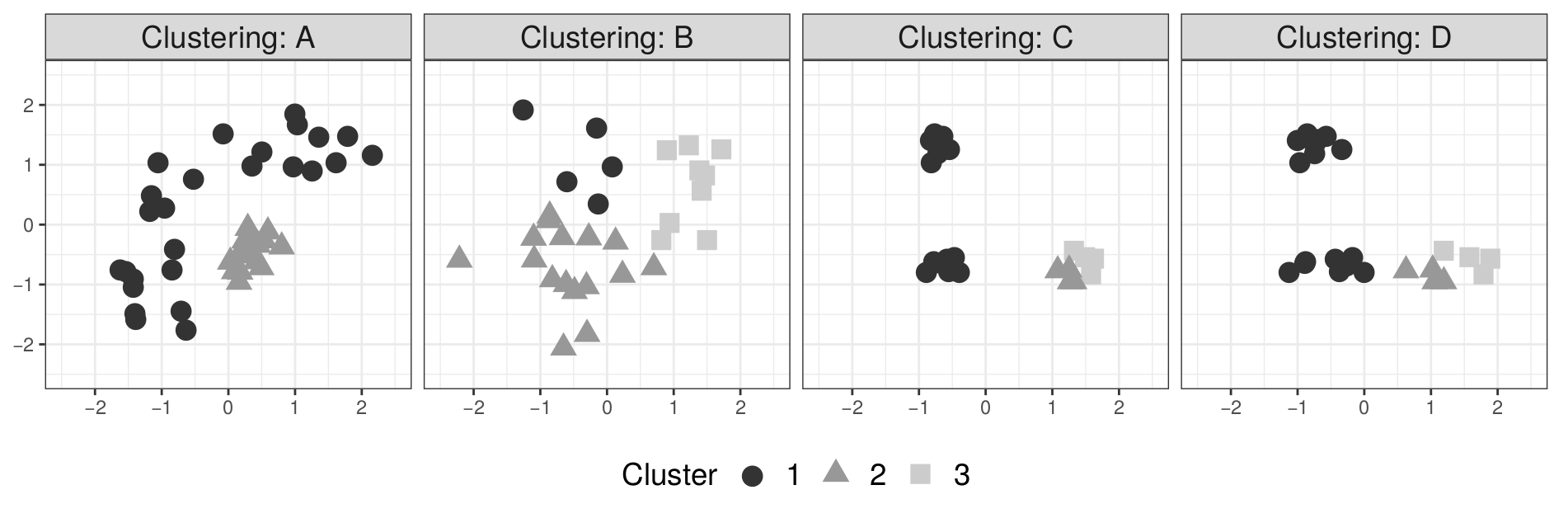
Aufgabe 3: Mögliche und Unmögliche k-Means-Ergebnisse#
Welche der folgenden Clusterings sind als Ergebnis einer konvergierten k-Means-Clusteranalyse möglich, welche sind unmöglich?