Data Science 1 (Hierarchisches Clustering) (Lösungen)

Im zweiten Teil dieses Tutoriums beschäftigen wir uns nun mit hierarchischem Clustering.

Hinweis: Aufgaben, die durch einen Asterisk (*) markiert sind, sind Bonusaufgaben. Diese Aufgaben können im Tutorium behandelt werden, dies ist jedoch von den Übungsleitern nicht geplant.

import time
import warnings
from itertools import cycle, islice

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sklearn
from scipy.cluster.hierarchy import dendrogram, linkage
from scipy.spatial import distance_matrix
from sklearn import cluster, mixture
from sklearn.datasets import load_iris
from sklearn.metrics import adjusted_rand_score

# Schriftfarbe für dark/light Mode Nutzer
# Bei Bedarf auf einen passenden Wert setzen
COLOR = "silver"

Aufgabe 3: Theorie

Ist hierarchisches Clustering ein distanzbasiertes Clusteringverfahren?

Musterlösung

Musterlösung

Hierarchisches Clustering ist wie viele andere Verfahren zur Datenanalyse ein distanzbasiertes Verfahren. Ein Cluster besteht dabei aus “Punkten”, die zueinander eine geringere Distanz aufweisen als zu den Punkten anderer Cluster.

Aufgabe 4: Dendrogramme zuordnen

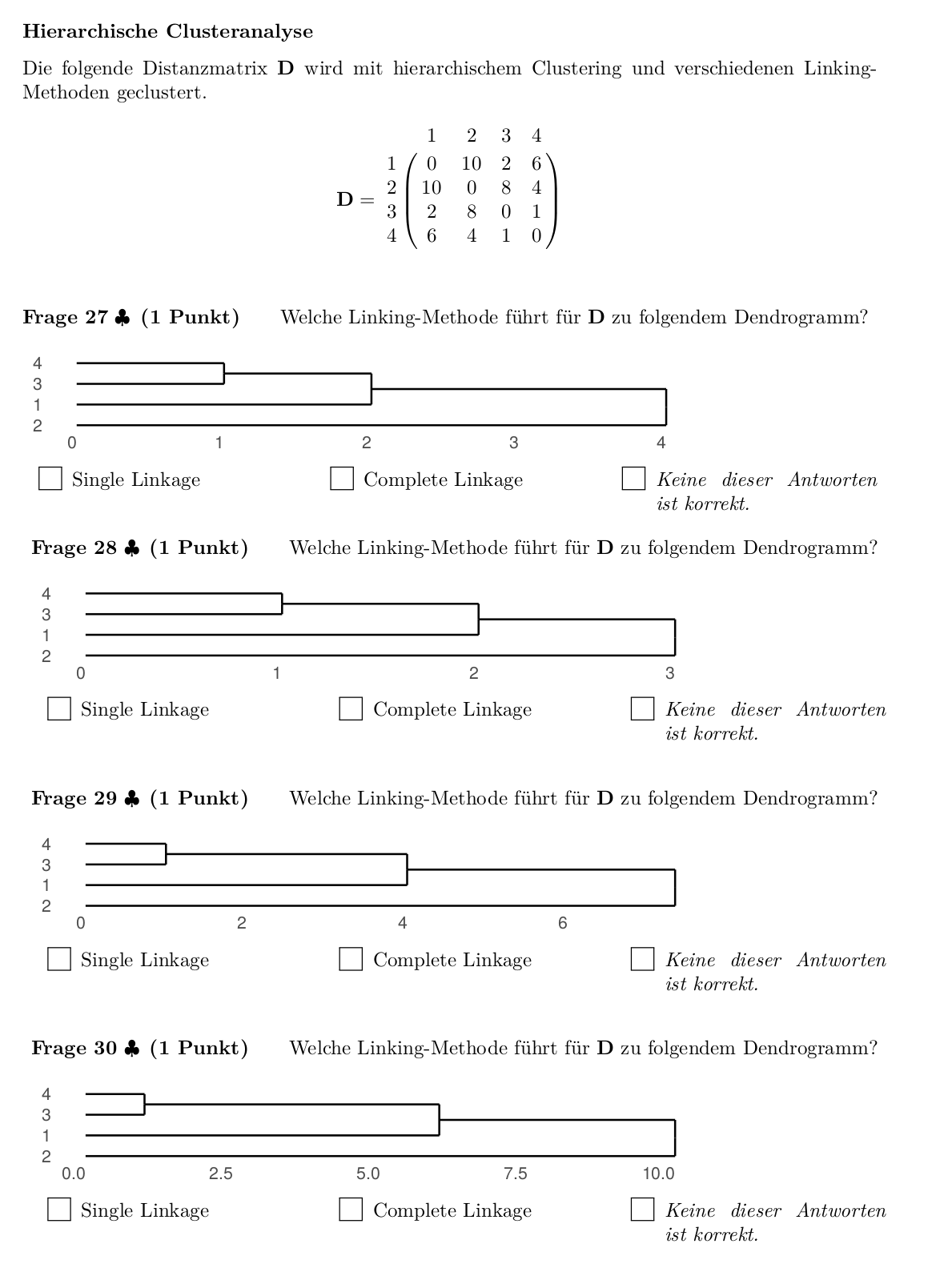
Hinweis: Es gibt verschiedene Varianten, bei welchem Wert Cluster-Verbindungen in ein Dendrogramm eingetragen werden. In der Vorlesung wurden Beispiele gezeigt, in denen Cluster-Verbindungen bei der Hälfte der Distanz eingetragen wurden (z.B., \(8.5\) für Distanz \(17\) auf Slide 8 von Vorlesung 9). Oben und im Folgenden verwenden wir die heute gängige Definition, bei der Cluster-Verbindungen bei der tatsächlichen Distanz eingetragen werden (im Beispiel von Slide 8 wäre das \(17\) für die Distanz \(17\)).

Musterlösung

Musterlösung:

• 27: single

• 28: keine

• 29: keine (das ist average)

• 30: complete

Aufgabe 5: Natürliche Zahlen Clustern

Wir nutzen hierarchische Clusteranalyse mit euklidischer Distanzfunktion, um die Menge der natürlichen Zahlen von 1 bis 512 (inklusive 1 und 512) zu clustern.

Falls mehrere Cluster dieselbe Distanz aufweisen, werden die zwei Cluster zusammengeführt, die die kleinste Zahl beinhalten. Wenn zum Beispiel Cluster \(A\) und \(B\) dieselbe Distanz zueinander haben wie Cluster \(C\) und \(D\), führen wir \(A\) und \(B\) zusammen, falls \(\operatorname{min}(A \cup B) < \operatorname{min}(C \cup D)\). Falls \(\operatorname{min}(A \cup B) = \operatorname{min}(C \cup D)\) entscheidet die nächstgrößere Zahl.

Wir interessieren uns dafür, wie groß die beiden Cluster sind, die wir als letztes zusammenführen (also die Cluster, die am Ursprung des Dendrogramms anliegen).

Fragen

1. Wie groß sind die letzten beiden Cluster für single linkage Clustering?

2. Wie groß sind die letzten beiden Cluster für complete linkage Clustering?

Musterlösung

Musterlösung

Hinweis: Hier bietet sich ein allgemeiner Vergleich der beiden linkage Methoden an.

Bei single linkage wählen wir basierend auf der geringsten Distanz zu irgendeinem Punkt eines Clusters und minimieren somit nur die Distanz zu irgendeinem Punkt und nicht zum gesamten Cluster. Bei complete linkage nehmen wir die geringste maximale Distanz zu einem Cluster, somit sind die daraus resultierenden Cluster tendenziell kompakter. Später sehen wir auch andere Methoden wie z.B. average (Durchschnitt) oder ward linkage.

1. 511 und 1

2. 256 und 256

Aufgabe 6: Hierarchisches Clustering üben

In dieser Aufgabe sollen Sie ein hierarchisches Clustering per Handsimulation auf zufällig generierten Datenpunkten durchführen. Dabei sollen Sie sowohl Single-Linkage als auch Complete-Linkage verwenden. Berechnen Sie dafür die Euklidische Distanz und runden Sie auf eine Nachkommastelle. Benutzen Sie den vorgegebenen Code, um die Datenpunkte für die Aufgabe zu erzeugen. Vergleichen Sie Ihre eigene Lösung mit der vorgegebenen Distanz-Matrix und dem Dendrogramm.

Achtung! Bei jeder Ausführung wird eine neue zufällige Kombination von Datenpunkten erzeugt. Diese Aufgabe eignet sich daher besonders zum selbstständigen Üben und zur Vorbereitung auf den Test.

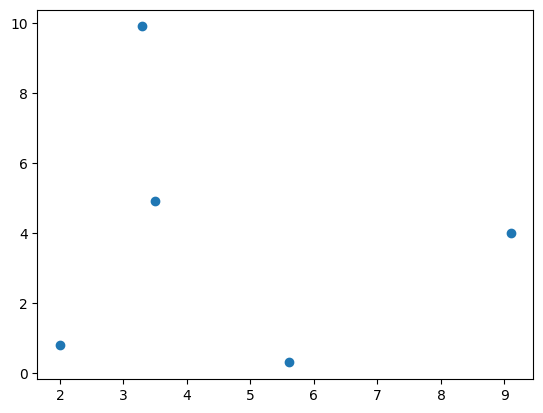
Zuerst werden die Datenpunkte für die Durchführung der Handsimulation erzeugt und visualisiert.

# Zufällige Kombination von Datenpunkten erzeugen
coords = (np.random.rand(5, 2) * 10).round(1)

# x- und y-Werte zuteilen
x = coords[:, 0]
y = coords[:, 1]

# Liste von Datenpunkte ausgeben
print(coords)

[[5.6 0.3]
 [2.  0.8]
 [9.1 4. ]
 [3.5 4.9]
 [3.3 9.9]]

# Datenpunkte visualisieren
plt.scatter(x, y)
plt.show()

Aufgabe 6.1

Erstellen Sie jetzt selbstständig die Distanz-Matrix für die vorgegebenen Datenpunkte, wobei die Abstände auf eine Nachkommastelle gerundet werden. Führen Sie den folgenden Code aus, um Ihre Lösung zu prüfen.

# Distanz-Matrix erstellen
print(distance_matrix(coords, coords).round(1))

[[0.  3.6 5.1 5.1 9.9]
 [3.6 0.  7.8 4.4 9.2]
 [5.1 7.8 0.  5.7 8.3]
 [5.1 4.4 5.7 0.  5. ]
 [9.9 9.2 8.3 5.  0. ]]

Aufgabe 6.2

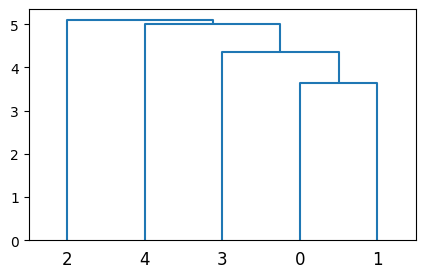
Führen Sie zuerst hierarchisches Clustering mit Single-Linkage und dann mit Complete-Linkage durch. Benutzen Sie den folgenden Code, um die Dendrogramme zu erstellen und Ihre Lösungen zu prüfen.

# Dendrogram für Single-Linkage Clustering
plt.figure(figsize=(5, 3))
dendrogram(linkage(coords, "single"))
plt.show()

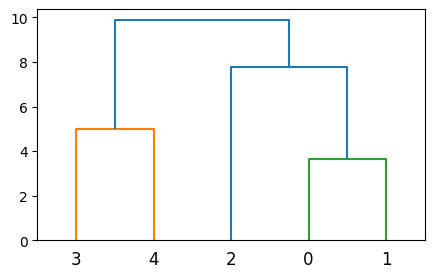
# Dendrogram für Complete-Linkage Clustering
plt.figure(figsize=(5, 3))
dendrogram(linkage(coords, "complete"))
plt.show()

Beispiel-Datenset: IRIS

Der IRIS-Datensatz beinhaltet 150 Datenpunkte von 4 Attributen von Schwertlilienpflanzen. Gemessen wurden jeweils Kelchblattlänge, Kelchblattbreite, Blütenblattlänge und Blütenblattbreite. Wir werden im Folgenden versuchen, die beobachteten Pflanzen zu clustern. Die Daten beinhalten zusätzlich auch die tatsächliche Art der Schwertlilien (Setosa, Versicolour oder Virginica). Somit können wir unser Clustering am Ende mit der “ground truth” vergleichen. Der Datensatz besteht also aus einer 150x4 Datenmatrix und einem 150x1 Labelvektor.

Iris Dataset importieren

# Datensatz laden
iris = load_iris()

# Das Objekt enthält Beobachtungen und Labels
iris.data[:10]  # wir geben hier nur die ersten 10 Beobachtungen aus

array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2],
       [5.4, 3.9, 1.7, 0.4],
       [4.6, 3.4, 1.4, 0.3],
       [5. , 3.4, 1.5, 0.2],
       [4.4, 2.9, 1.4, 0.2],
       [4.9, 3.1, 1.5, 0.1]])

# Sowie die möglichen Label
list(iris.target_names)

[np.str_('setosa'), np.str_('versicolor'), np.str_('virginica')]

Einführung in Hierarchisches Clustering mit scikit-learn

In dieser Aufgabe werden Sie die Hierarchical Clustering Implementierung von scikit-learn nutzen, um das IRIS-Datenset mit verschiedenen Linking-Methoden zu clustern.

Im Folgenden geben wir Ihnen ein Beispiel, wie die scikit-learn Implementierung angewandt wird. Ihre Aufgabe ist es, verschiedene Linking-Methoden anzuwenden und die sich ergebenden Clusterings zu vergleichen.

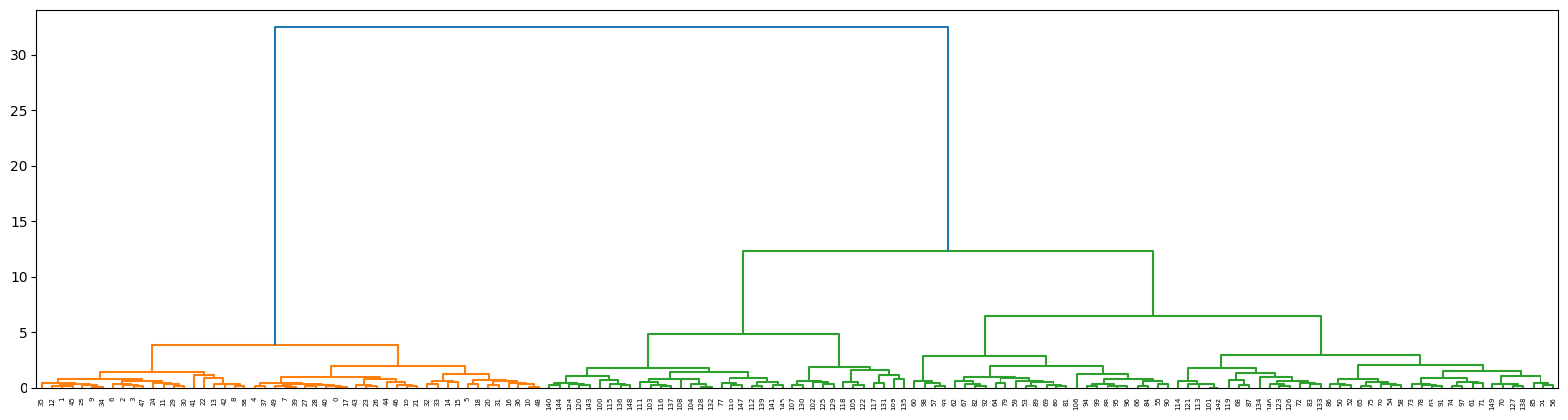
# Führt Hierarchisches Clustering durch und zeichnet das Dendrogramm
linkage_matrix = linkage(iris.data, "ward")
plt.figure(figsize=(20, 5))
dendrogram(linkage_matrix)
plt.show()

# Führt hierarchisches Clustering bis zu einer gegebenen Zahl von Clustern durch
# und gibt Cluster-Assignments für jeden Datenpunkt zurück
assignments = cluster.AgglomerativeClustering(n_clusters=3, linkage="ward").fit_predict(iris.data)
assignments

array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2,
       2, 2, 2, 0, 0, 2, 2, 2, 2, 0, 2, 0, 2, 0, 2, 2, 0, 0, 2, 2, 2, 2,
       2, 0, 0, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 0])

Aufgabe 7: Dendrogramme interpretieren

Interpretieren Sie das aus der Einführung entstandene Dendrogramm.

• Was stellt die x-Achse dar?

• Was stellt die y-Achse dar?

Musterlösung

Musterlösung

Die vertikale Achse des Dendrogramms stellt den Abstand beziehungsweise die “Unähnlichkeit” zwischen den Clustern dar. Die horizontale Achse stellt die Objekte und Cluster dar.
Jede Verbindung (Fusion) von zwei Clustern wird auf dem Diagramm durch die Teilung einer vertikalen Linie in zwei vertikale Linien dargestellt. Die vertikale Position der Teilung, die durch den kurzen horizontalen Balken angezeigt wird, gibt den Abstand (Unähnlichkeit) zwischen den beiden Clustern an.

Aufgabe 8: Vergleich verschiedener Linkage-Methoden*

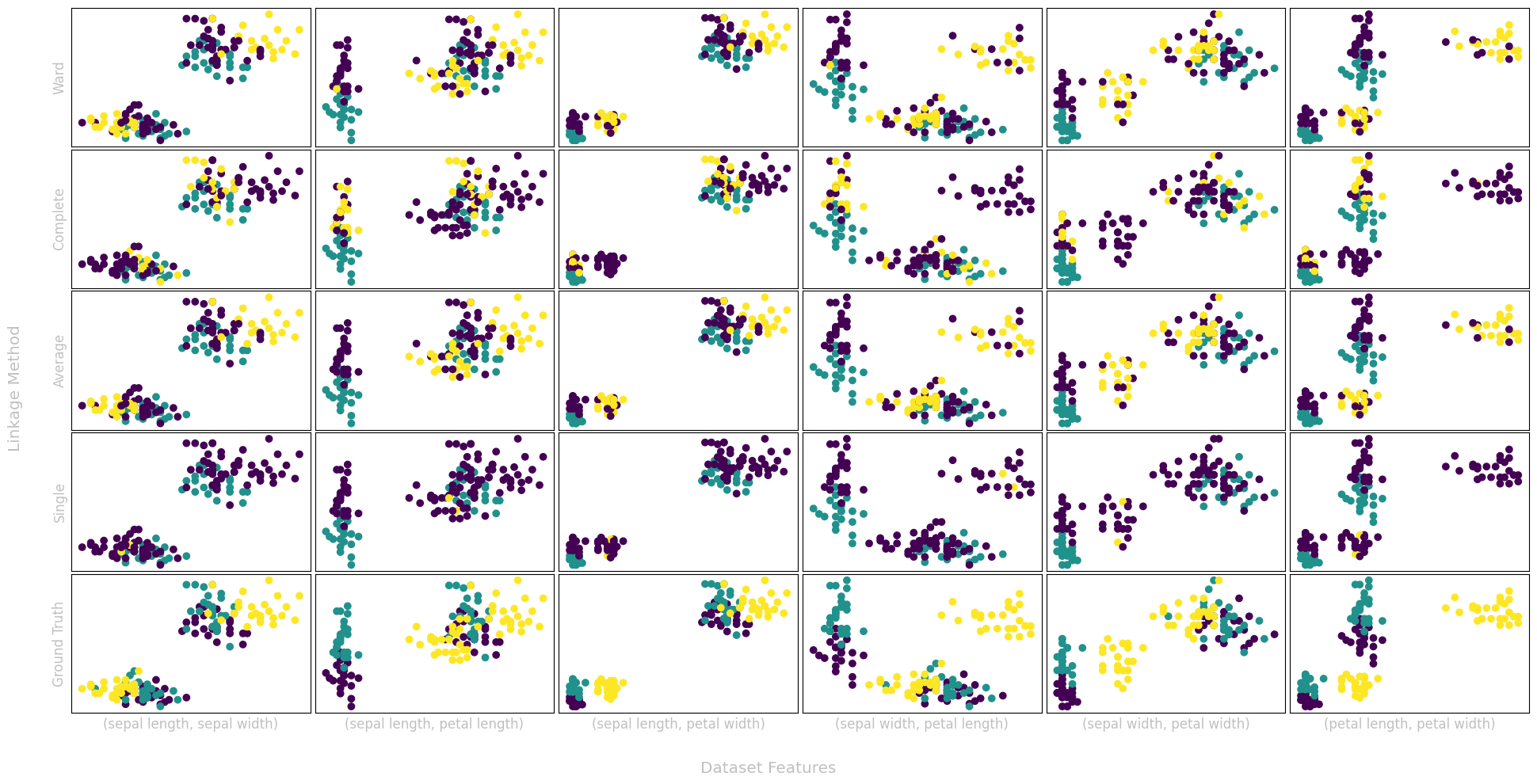
Der unten stehende Code generiert zuerst hierarchische Clusterings mit unterschiedlichen Linkage-Methoden. Zusätzlich zu den in der Vorlesung vorgestellten Methoden wird hier auch Ward und average Linkage berechnet. Da wir wissen, dass es drei Klassen der Pflanze gibt, lassen wir scikit-learn mittels der diversen Linkage-Methoden drei Cluster bilden.

Vergleichen Sie verschiedene Verknüpfungskriterien (“linkage methods”) für den IRIS-Datensatz, d.h. neben “single” und “complete” auch “ward” und “average”, indem Sie verschiedene Feature-Kombinationen plotten und die Punkte entsprechend ihres Clusters einfärben.

• Was sind die konzeptionellen Unterschiede zwischen den Methoden?

• Welches der Kriterien kommt Ihrer Meinung nach am nähsten an die “ground truth” Cluster-Assignments heran?

Hinweis: Vergleichen Sie hierzu auch die Cluster-Assignments des hierarchischen Clusterings (assignments_<type>) mit den tatsächlichen Clustern (iris.target). Speichern Sie die Cluster-Assignments der verschiedenen Methoden (z.B., als assignments_ward, assignments_complete, …).

Hinweis: Das Ward-Linkage minimiert die Varianz innerhalb eines Clusters.

assignments_ward = cluster.AgglomerativeClustering(n_clusters=3, linkage="ward").fit_predict(
    iris.data
)
assignments_complete = cluster.AgglomerativeClustering(
    n_clusters=3, linkage="complete"
).fit_predict(iris.data)
assignments_average = cluster.AgglomerativeClustering(n_clusters=3, linkage="average").fit_predict(
    iris.data
)
assignments_single = cluster.AgglomerativeClustering(n_clusters=3, linkage="single").fit_predict(
    iris.data
)

fig, axes = plt.subplots(5, 6, figsize=(20, 10))
plt.subplots_adjust(left=0.06, right=0.98, bottom=0.09, top=0.98, wspace=0.02, hspace=0.02)

for i, (assignments, name) in enumerate(
    [
        (assignments_ward, "Ward"),
        (assignments_complete, "Complete"),
        (assignments_average, "Average"),
        (assignments_single, "Single"),
        (iris.target, "Ground Truth"),
    ]
):
    for j, features in enumerate([(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)]):
        axes[i][j].scatter(*np.split(iris.data[:, (features)], 2), c=assignments)
        if j == 0:
            axes[i][j].set_ylabel(name, size="large", color=COLOR)
        if i == 4:
            axes[i][j].set_xlabel(
                f"({iris.feature_names[features[0]][:-5]}, {iris.feature_names[features[1]][:-5]})",
                size="large",
                color=COLOR,
            )
        axes[i][j].set_xticks([])
        axes[i][j].set_yticks([])

fig.supxlabel("Dataset Features", size="x-large", color=COLOR)
fig.supylabel("Linkage Method", size="x-large", color=COLOR)
plt.show()

Musterlösung

Musterlösung

Single und complete linkage haben oftmals starke Abweichungen von der tatsächlichen Kategorisierung, wobei single linkage oftmals noch schlechter funktioniert, als complete linkage. Dies liegt daran, dass ein neuer Punkt, der zu einem Cluster hinzugefügt wird, nur einem anderen Punkt ähneln muss und nicht dem Cluster. Complete linkage fordert stattdessen, dass der neue Punkt auch möglichst nah zum maximal entferntesten Punkt sein muss. Wir nutzen diese nur, da sie einfach zu berechnen sind. Average und ward linkage funktionieren wesentlich besser und repräsentieren meistens die tatsächlichen Label, wobei auch diese natürlich Fehler beinhalten.

Aufgabe 9: Systematischer Vergleich der Assignments

Cluster-Assignments manuell zu vergleichen ist mühsam, besonders bei großen Datensätzen. Wir werden nun die Metrik adjusted_rand_score nutzen, um die Assignments jeder Methode zu beurteilen. Die Metrik gibt einen Cluster-Validierungsindex zurück, der zwischen -1 und 1 liegt, wobei 1 bedeutet, dass zwei Clusterings identisch sind (unabhängig davon, welches Label jedem Cluster zugeordnet ist).

Unten werden die Scores beispielhaft berechnet und dann für unseren konkreten Datensatz. Was kann bzgl. der Qualität unserer Linkage-Methoden gesagt werden?

# Beispiel:
ground_truth = [0, 0, 1, 1, 2, 2]
assignments_good_clustering = [1, 1, 2, 2, 0, 0]
assignments_bad_clustering = [0, 1, 2, 0, 1, 2]
print(f"Guter Score: {adjusted_rand_score(ground_truth, assignments_good_clustering)}")
print(f"Schlechter Score: {adjusted_rand_score(ground_truth, assignments_bad_clustering)}")

Guter Score: 1.0
Schlechter Score: -0.25

pd.DataFrame.from_dict(
    {
        "ward": (adjusted_rand_score(iris.target, assignments_ward),),
        "complete": (adjusted_rand_score(iris.target, assignments_complete),),
        "average": (adjusted_rand_score(iris.target, assignments_average),),
        "single": (adjusted_rand_score(iris.target, assignments_single),),
    }
).style.hide(axis="index")

ward	complete	average	single
0.731199	0.642251	0.759199	0.563751

Musterlösung

Musterlösung

Es wird bestätigt, dass single linkage am schlechtesten funktioniert und nicht sonderlich geeignet ist. Dafür wie einfach complete linkage ist, funktioniert es schon besser. Das ist naheliegend, da es nicht nach einem Extremum sucht, dem es ähnlich ist, sondern den Punkt, der am unählichsten ist und wo gleichzeitig die Distanz im Cluster-Vergleich minimal ist. Zuletzt kann gesagt werden, dass Ward und average nochmal besser funktionieren, aber trotzdem nicht den Wert 1 annehmen, da Machine Learning nur in den aller wenigsten Fällen perfekte Kategorisierung erreichen kann.

Aufgabe 10: Clustering-Algorithmen*

Wir haben in diesem Modul zwei Cluster-Verfahren kennengelernt: k-Means und hierarchisches Clustering. Darüber hinaus gibt es viele weitere Clustering-Verfahren. Nachfolgend ist ein Vergleich der verschiedenen Clustering-Verfahren in scikit-learn auf verschiedenen Datensätzen implementiert. Weitere Informationen

Konstruktion der Datensätze

np.random.seed(0)
n_samples = 1500

# Datasets 1-4
noisy_circles = sklearn.datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.05)
noisy_moons = sklearn.datasets.make_moons(n_samples=n_samples, noise=0.05)
blobs = sklearn.datasets.make_blobs(n_samples=n_samples, random_state=8)
no_structure = np.random.rand(n_samples, 2), None

# 5. Dataset: Anisotropisch verteilte Daten
random_state = 170
X, y = sklearn.datasets.make_blobs(n_samples=n_samples, random_state=random_state)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_aniso = np.dot(X, transformation)
aniso = (X_aniso, y)

# 6. Dataset: 'Kleckse' mit unterschiedlichen Varianzen
varied = sklearn.datasets.make_blobs(
    n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
)

default_base = {
    "quantile": 0.3,
    "eps": 0.3,
    "damping": 0.9,
    "preference": -200,
    "n_neighbors": 10,
    "n_clusters": 3,
    "min_samples": 20,
    "xi": 0.05,
    "min_cluster_size": 0.1,
}

datasets = [
    (
        noisy_circles,
        "Noisy Circles",
        {
            "damping": 0.77,
            "preference": -240,
            "quantile": 0.2,
            "n_clusters": 2,
            "min_samples": 20,
            "xi": 0.25,
        },
    ),
    (
        noisy_moons,
        "Noisy Moons",
        {"damping": 0.75, "preference": -220, "n_clusters": 2},
    ),
    (blobs, "Blobs", {}),
    (no_structure, "No Structure", {}),
    (
        aniso,
        "Anisotropic",
        {
            "eps": 0.15,
            "n_neighbors": 2,
            "min_samples": 20,
            "xi": 0.1,
            "min_cluster_size": 0.2,
        },
    ),
    (
        varied,
        "Varied",
        {
            "eps": 0.18,
            "n_neighbors": 2,
            "min_samples": 5,
            "xi": 0.035,
            "min_cluster_size": 0.2,
        },
    ),
]

Anwendung von verschiedenen Cluster-Verfahren

Hinweis: Das Ausführen der unten stehenden Codezelle braucht etwas länger.

for i, (dataset, d_name, d_params) in enumerate(datasets):
    # Aktualisierung der Parameter mit datensatzspezifischen Werten
    params = default_base.copy()
    params.update(d_params)
    X, y = dataset

    # Datensätze normalisieren, um die Parameterauswahl zu erleichtern
    X = sklearn.preprocessing.StandardScaler().fit_transform(X)

    # Bandbreite für 'mean shift' schätzen
    bandwidth = cluster.estimate_bandwidth(X, quantile=params["quantile"])

    # Konnektivitätsmatrix für strukturierte 'structured Ward'
    connectivity = sklearn.neighbors.kneighbors_graph(
        X, n_neighbors=params["n_neighbors"], include_self=False
    )

    # Konnektivität symmetrisch machen
    connectivity = 0.5 * (connectivity + connectivity.T)

    # Cluster-Objekte mit Hilfe der Datasets I. - VI. erstellen
    k_means = cluster.MiniBatchKMeans(n_clusters=params["n_clusters"], init="random", n_init=1)
    ward = cluster.AgglomerativeClustering(
        n_clusters=params["n_clusters"], linkage="ward", connectivity=connectivity
    )
    affinity_propagation = cluster.AffinityPropagation(
        damping=params["damping"], preference=params["preference"]
    )
    ms = cluster.MeanShift(bandwidth=bandwidth, bin_seeding=True)
    spectral = cluster.SpectralClustering(
        n_clusters=params["n_clusters"],
        eigen_solver="arpack",
        affinity="nearest_neighbors",
    )
    average_linkage = cluster.AgglomerativeClustering(
        linkage="average",
        metric="manhattan",
        n_clusters=params["n_clusters"],
        connectivity=connectivity,
    )
    dbscan = cluster.DBSCAN(eps=params["eps"])
    optics = cluster.OPTICS(
        min_samples=params["min_samples"],
        xi=params["xi"],
        min_cluster_size=params["min_cluster_size"],
    )
    birch = cluster.Birch(n_clusters=params["n_clusters"])
    gmm = mixture.GaussianMixture(n_components=params["n_clusters"], covariance_type="full")

    # Speichern der Algorithmus-Parameter/Cluster-Objekte
    clustering_algorithms = (
        ("MiniBatch\nKMeans", k_means),
        ("Affinity\nPropagation", affinity_propagation),
        ("Ward", ward),
        ("MeanShift", ms),
        ("Spectral\nClustering", spectral),
        ("Agglomerative\nClustering", average_linkage),
        ("DBSCAN", dbscan),
        ("OPTICS", optics),
        ("BIRCH", birch),
        ("Gaussian\nMixture", gmm),
    )

    # Visualisierung der Ergebnisse
    plt.figure(figsize=(21, 12.5))
    plt.subplots_adjust(left=0.02, right=0.98, bottom=0.001, top=0.96, wspace=0.05, hspace=0.01)

    for j, (a_name, algorithm) in enumerate(clustering_algorithms):
        t0 = time.time()

        # Warnungen bei langen Laufzeiten
        with warnings.catch_warnings():
            warnings.filterwarnings(
                "ignore",
                message="the number of connected components of the connectivity"
                + " matrix is [0-9]{1,2} > 1. Completing it to avoid stopping the tree early.",
                category=UserWarning,
            )
            warnings.filterwarnings(
                "ignore",
                message="Graph is not fully connected, spectral embedding"
                + " may not work as expected.",
                category=UserWarning,
            )
            warnings.filterwarnings(
                "ignore",
                message="Affinity propagation did not converge, this model may"
                + " return degenerate cluster centers and labels.",
                category=sklearn.exceptions.ConvergenceWarning,
            )

            algorithm.fit(X)

        t1 = time.time()
        if hasattr(algorithm, "labels_"):
            y_pred = algorithm.labels_.astype(int)
        else:
            y_pred = algorithm.predict(X)

        plt.subplot(len(datasets), len(clustering_algorithms), j + 1)
        if i == 0:
            plt.title(a_name, size=18, color=COLOR)
        if j == 0:
            plt.ylabel(d_name, size=18, color=COLOR)

        # Farbpalette
        colors = np.array(
            list(
                islice(
                    cycle(
                        [
                            "#377eb8",
                            "#ff7f00",
                            "#4daf4a",
                            "#f781bf",
                            "#a65628",
                            "#984ea3",
                            "#999999",
                            "#e41a1c",
                            "#dede00",
                        ]
                    ),
                    int(max(y_pred) + 1),
                )
            )
        )
        # Schwarze Farbe für Ausreißer hinzufügen (falls vorhanden)
        colors = np.append(colors, ["#000000"])

        plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])

        plt.xlim(-2.5, 2.5)
        plt.ylim(-2.5, 2.5)
        plt.xticks(())
        plt.yticks(())
        plt.text(
            0.99,
            0.01,
            ("%.2fs" % (t1 - t0)).lstrip("0"),
            transform=plt.gca().transAxes,
            size=15,
            horizontalalignment="right",
        )

plt.show()

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[16], line 92
     79     warnings.filterwarnings(
     80         "ignore",
     81         message="Graph is not fully connected, spectral embedding"
     82         + " may not work as expected.",
     83         category=UserWarning,
     84     )
     85     warnings.filterwarnings(
     86         "ignore",
     87         message="Affinity propagation did not converge, this model may"
     88         + " return degenerate cluster centers and labels.",
     89         category=sklearn.exceptions.ConvergenceWarning,
     90     )
---> 92     algorithm.fit(X)
     94 t1 = time.time()
     95 if hasattr(algorithm, "labels_"):

File /usr/local/lib/python3.13/site-packages/sklearn/base.py:1365, in _fit_context.<locals>.decorator.<locals>.wrapper(estimator, *args, **kwargs)
   1358     estimator._validate_params()
   1360 with config_context(
   1361     skip_parameter_validation=(
   1362         prefer_skip_nested_validation or global_skip_validation
   1363     )
   1364 ):
-> 1365     return fit_method(estimator, *args, **kwargs)

File /usr/local/lib/python3.13/site-packages/sklearn/cluster/_affinity_propagation.py:537, in AffinityPropagation.fit(self, X, y)
    529 preference = np.asarray(preference)
    531 random_state = check_random_state(self.random_state)
    533 (
    534     self.cluster_centers_indices_,
    535     self.labels_,
    536     self.n_iter_,
--> 537 ) = _affinity_propagation(
    538     self.affinity_matrix_,
    539     max_iter=self.max_iter,
    540     convergence_iter=self.convergence_iter,
    541     preference=preference,
    542     damping=self.damping,
    543     verbose=self.verbose,
    544     return_n_iter=True,
    545     random_state=random_state,
    546 )
    548 if self.affinity != "precomputed":
    549     self.cluster_centers_ = X[self.cluster_centers_indices_].copy()

File /usr/local/lib/python3.13/site-packages/sklearn/cluster/_affinity_propagation.py:103, in _affinity_propagation(S, preference, convergence_iter, max_iter, damping, verbose, return_n_iter, random_state)
    100 R += tmp
    102 # tmp = Rp; compute availabilities
--> 103 np.maximum(R, 0, tmp)
    104 tmp.flat[:: n_samples + 1] = R.flat[:: n_samples + 1]
    106 # tmp = -Anew

KeyboardInterrupt: 

Aufgabe 10.1

k-Means läuft (fast immer) schneller als hierarchisches Clustering (siehe Laufzeiten unten rechts in den Bildern). Warum?

Musterlösung

Musterlösung

Weil k-Means ein Clustering bestimmt und hierarchisches Clustering ein Dendrogramm von vielen Clusterings bestimmt, somit ist die Zeitkomplexität von k-Means linear, während die von hierarchischem Clustering quadratisch ist.

Aufgabe 10.2

Welche Limitierungen von k-Means können Sie gegenüber hierarchischem Clustering erkennen?

Musterlösung

Musterlösung

Nachteile von k-Means:

• Da wir k-Means Clustering mit einer zufälligen Auswahl von Clustern beginnen, können die Ergebnisse, die durch mehrmaliges Ausführen des Algorithmus erzeugt werden, unterschiedlich sein. Die Ergebnisse beim hierarchischen Clustering hingegen sind reproduzierbar.

• Es hat sich gezeigt, dass k-Means gut funktioniert, wenn die Form der Cluster hypersphärisch ist (z.B. Kreis in 2D, Kugel in 3D). Andererseits ist es schlechter, wenn dies nicht gegeben ist.

• k-Means-Clustering erfordert Vorkenntnisse über k, d.h. es ist eine Anzahl von Clustern erforderlich, in die Sie Ihre Daten unterteilen möchten.

Aufgabe 10.3

Welche Vor- und Nachteile erkennen Sie bei den anderen Clustering-Algorithmen?

Musterlösung

Musterlösung

Ähnlich, wie in Aufgabe 10.2, sind unter anderem die Laufzeiten der Algorithmen sehr unterschiedlich. Während k-Means meist nur 0.01s benötigt, brauchen manche dieser Clustering-Algorithmen mehr als eine Sekunde pro Clustering. Dafür bieten manche von diesen auch stabile Ergebnisse, in der Hinsicht, dass Sie die Gruppen “finden”, welche wir auch mit dem Auge gut sehen können (wobei k-Means zum Teil scheitert). Allerdings ist dies nicht garantiert. Während z.B. DBSCAN und OPTICS oftmals gute Ergebnisse liefern, sehen wir z.B. auch, dass Affinity Propagation oftmals schlechte Clusterings liefert und dies trotz langer Laufzeiten.